Hypotenuse Calculator

The hypotenuse of a right-angled triangle is the longest of its three sides. In a right-angled triangle, the angle between the two sides apart from the hypotenuse is 90°.

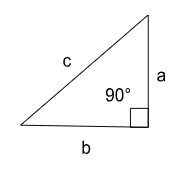
In the above figure, ‘c’ is the hypotenuse, while ‘a’ and ‘b’ are the sides with a right angle (90°) between them.

The lengths of the three sides of a right-angled triangle are connected by an equation termed as the Pythagoras theorem. If you find it tough to do this calculation, you can use our hypotenuse calculator to calculate the length of the hypotenuse of a triangle.

The hypotenuse calculator is useful for calculating the length of a right-angled triangle’s hypotenuse. Follow these simple steps to learn how to calculate hypotenuse of a triangle in a jiffy.

1. Enter the value of side ‘a’ (a>0) in the first input text box.
2. Enter the value of side ‘b’ (b>0) in the second input text box.
3. Press the Calculate button.
4. Now, you get the length of the hypotenuse from the calculator.

Scroll further to learn how to find the hypotenuse of a right triangle.

The Pythagoras theorem is the solution for how to find the hypotenuse of a right triangle. According to this theorem, the length of the hypotenuse is the square root of the added squares of the other two sides of the right-angled triangle.

c = √( a2 +b2)

Where a >= 1 and b>=1 and all of a,b,c have the same metric units.

The values of a,b, and c are termed as Pythagorean triplets.

Case 1

Consider the following example. Let a = 4, b = 3, then the hypotenuse is calculated as

c = √( a2 +b2) = √( 42 +32) = √( 16 +9) = √25 = 5

So, the hypotenuse of a triangle with sides 4 units and 3 units is 5 units. The numbers 3,4, and 5 are termed as a Pythagorean triplet.

Case 2

Similarly, you can also input decimal values in the hypotenuse calculator.

Consider a = 5.5, b = 2.5, then the hypotenuse is

c = √( a2 +b2) = √( (5.5)2 +(2.5)2) = √( 30.25 +6.25) = √36.5 = 6.041

The hypotenuse of a right-angled triangle with sides 5.5 units and 2.5 units is 6.041 units.

Case 3

You can also compute the length of the hypotenuse of a right-angled isosceles triangle. In an isosceles right triangle, two sides are equal, i.e., a=b.

Consider the length of the equal sides as 8 units.

c = √( a2 +b2) = √( 82 +82) = √( 64 +64) = √128 = 11.31

The hypotenuse of a right-angled isosceles triangle with equal sides measuring 8 units each, is 11.31 units.

1. When trying to reach something at a height, you can use this calculator to determine the length of a ladder required to reach the object.
2. Mariners can calculate the hypotenuse to get the distance to navigate between two locations with their coordinates.
3. You can compute diagonals of shapes such as squares, cubes, cuboids, prisms, etc.
4. One can calculate the distance between prominent city buildings to draw a skyline.